数据库八股文——关系代数

简单专门关系代数

关系代数是施加于关系之上的一组集合代数运算，每个运算都以一个或多个关系作为运算对象，并生成另外一个关系作为该关系运算的结果。

选择运算

选择运算为一元运算，其中 p 为谓词语句，R 为输入的关系，结果是 R 中所有符合谓词语句 p 的元组构成的新关系。

投影运算

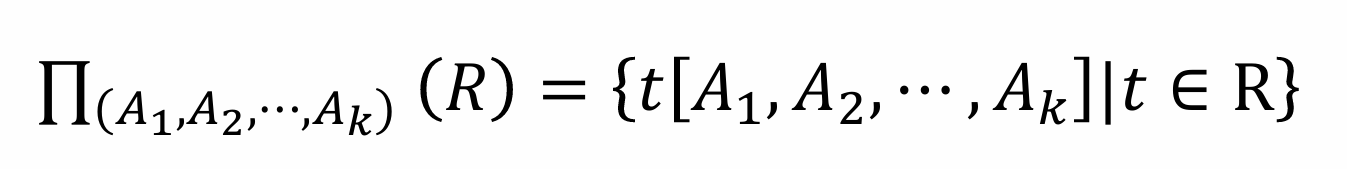
投影运算为一元运算，其中 (A₁, A₂, …, A_n) 为输入的属性列表，R 为输入的关系，结果是 R 中所有元组的 A₁, A₂, …, A_n 列构成的新关系。

复杂专门关系代数

重命名运算

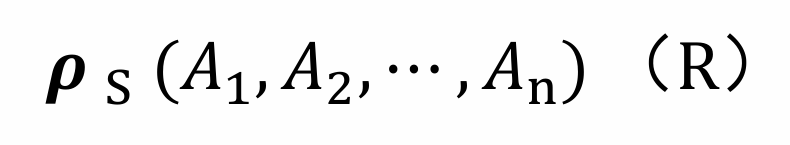
重命名运算为一元运算，其中 R 为输入的关系，S 为要修改的关系名，(A₁, A₂, …, A_n) 为依次要修改的属性名。
也可以不传入 (A₁, A₂, …, A_n) 参数，表示只需要修改关系名。

有点巧妙，放这里了
查找最高工资的关系代数表达式：

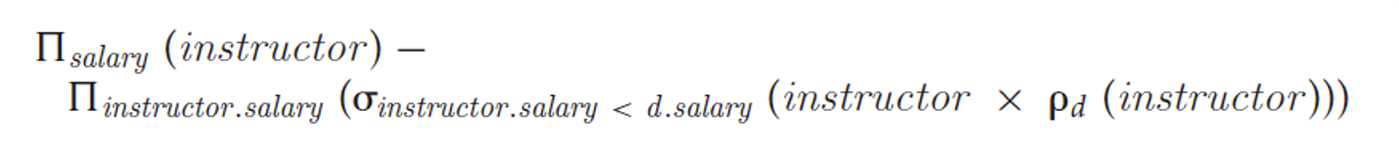
通过位置标记也可以获取第 i 个属性，使用关键字 $。

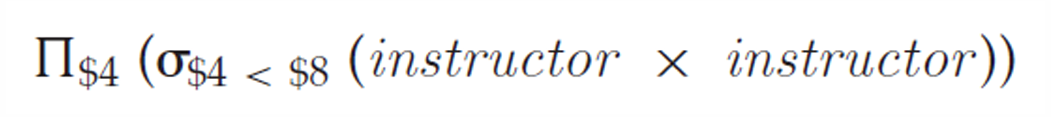
连接运算

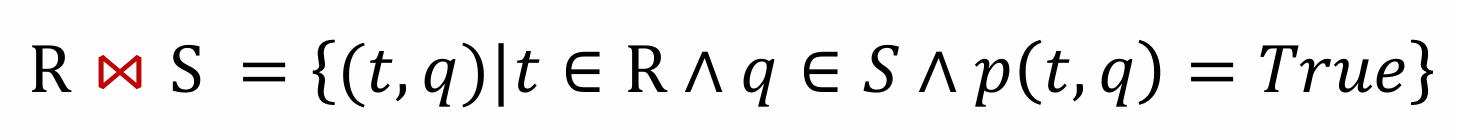
第一种连接

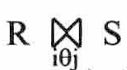
先求笛卡尔积，再进行选择运算，其中选择运算的谓词语句和连接的谓词语句相同。

第二种连接

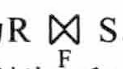
先求笛卡尔积，再进行选择运算，其中选择运算的谓词语句和连接的谓词语句相同。

自然连接

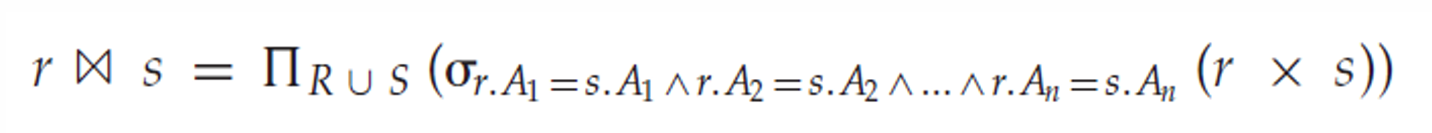
先求笛卡尔积，再找到 R 和 S 的公共属性，例如为 (A₁, A₂, …, A_n)，通过谓词语句 R.A₁ = S.A₁ … R.A_n = S.A_n 筛选出符合要求的元组。

对于两个关系 R, S，我们称 R 的悬浮元组为不满足 R.A₁ = S.A₁ … R.A_n = S.A_n 的元组，S 同理。

外连接 可以将悬浮元组保留表中，在其他属性上填写 NULL。
左外连接 可以将左关系 R 悬浮元组保留表中，在其他属性上填写 NULL。
右外连接 可以将右关系 S 悬浮元组保留表中，在其他属性上填写 NULL。

自然连接结果属性出现的顺序为：相同属性 > 只属于第一个关系的属性 > 只属于第二个关系的属性。

代数运算表示，但是我不想看：

赋值运算

E 为关系代数表达式，T 为临时关系变量，通过赋值运算可以分解复杂的关系代数表达式，使查询变得简单。

除运算

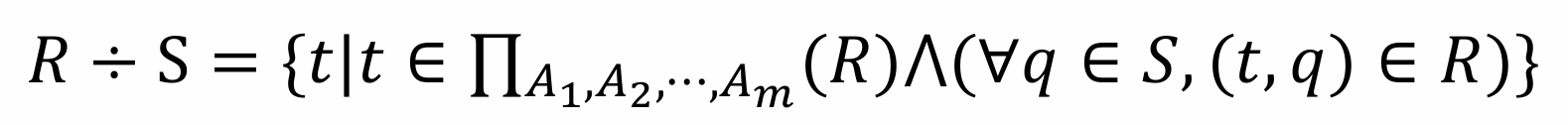
假设有两个关系 R(X, Y), S(Z) 其中，Y 和 Z 有相容性。

则 R(X, Y) ÷ S(Z) 为：
1 结果的属性集为 X，且是 R 中 X 的一个子集
2 保留下来的元组和 S(Z) 求笛卡尔积，得到的结果必须包含于 R(X, Y)
3 S 中的属性必须包含于 R 中

去重运算

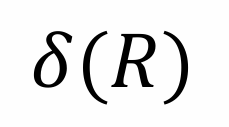
去重运算可以去除关系中的重复元组，并返回去重之后的关系。

广义投影运算

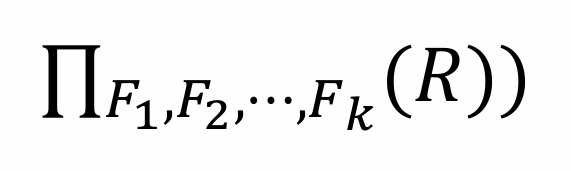
允许在投影列表中使用算术运算和字符串函数等来对投影运算进行扩展，写过 miniob 都说好。

聚集运算

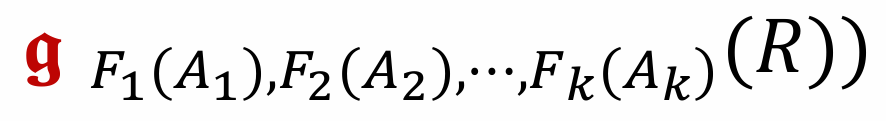
其中 A₁, A₂, …, A_k 为 R 中的属性列，F 为作用在属性 A 上的聚集函数，例如 count, sum, avg, min, max 等。

通过书法体 G 还可以完成 SQL 语句中的 GROUP BY 功能。

通过 distinct 关键字也可以完成去重功能，例如聚集函数 count-distionct。

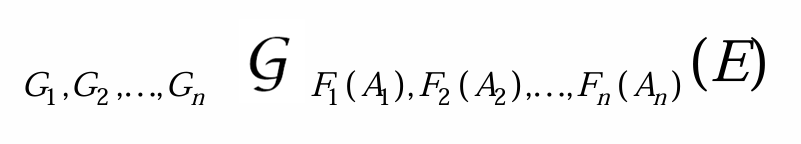
其中 G₁, G₂, …, G_n 为属性集合，要求根据属性集合分组后，同一组的属性集合取值一样，不同组的属性集合取值不一样。也即，各组属性可以通过 G₁, G₂, …, G_n 来唯一区分。

G₁, G₂, …, G_n 为可选参数，如果不填写该参数，将所有元组视作一个组别。

排序运算

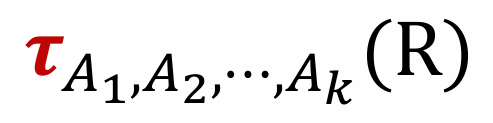
其中 A₁, A₂, …, A_k 为 R 中的属性列，按照顺序依次对元组进行排序。

传统集合运算

关系的相容性

关系 R 和 关系 S 相容的充分必要条件是：

1. R 和 S 中的属性个数相同
2. R 和 S 中属性存在一一对应关系
3. R 和 S 中的对应属性的域相同

并运算

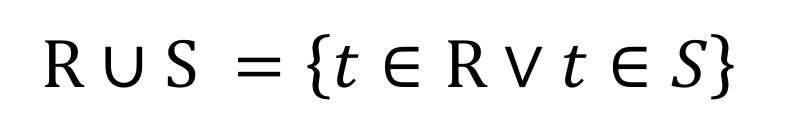
并运算为二元运算，其中 R, S 为输入的两个相容关系，结果是 R 和 S 的并集。

交运算

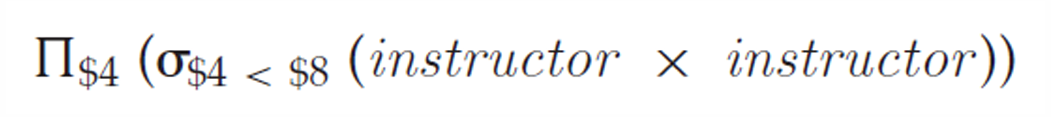
交运算为二元运算，其中 R, S 为输入的两个相容关系，结果是 R 和 S 的交集。

差运算

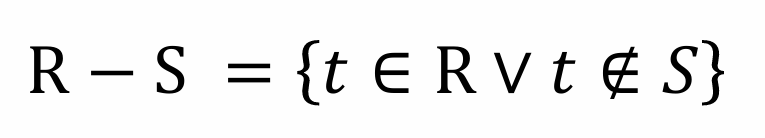
差运算为二元运算，其中 R, S 为输入的两个相容关系，结果是 R 和 S 的差集。

笛卡儿积运算

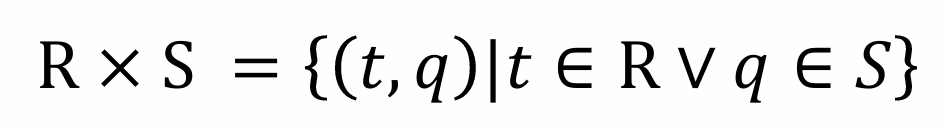
笛卡儿积运算为二元运算，其中 R, S 为输入的两个关系，结果是 R 和 S 的笛卡尔积。
若关系 R 是 m 度关系，有 x 个元组；关系 S 是 n 度关系，有 y 个元组；则笛卡尔积为 m + n 度关系，元组个数为 x × y。

换句话说，一个关系一定是：其所有属性的域的笛卡儿积的一个子集。

关系演算语言

元组关系演算语言

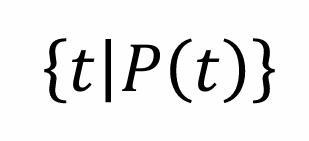
P 是原子公式，有以下三种形式：

其中 t 为元组变量，R 为关系。

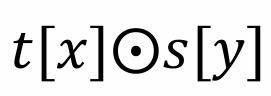
其中 t, s 为元组变量，x, y 为关系中在元组 t, s 下的属性。

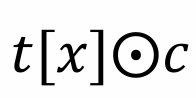
其中 c 是属于 x 域中的常量。

域关系演算语言

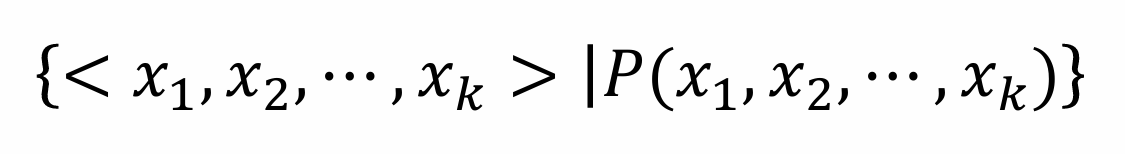
其中 x₁, x₂, …, x_k 是域变量或者域常量。

元组关系演算语言和域关系演算语言不是很好理解，下面附上一道例题

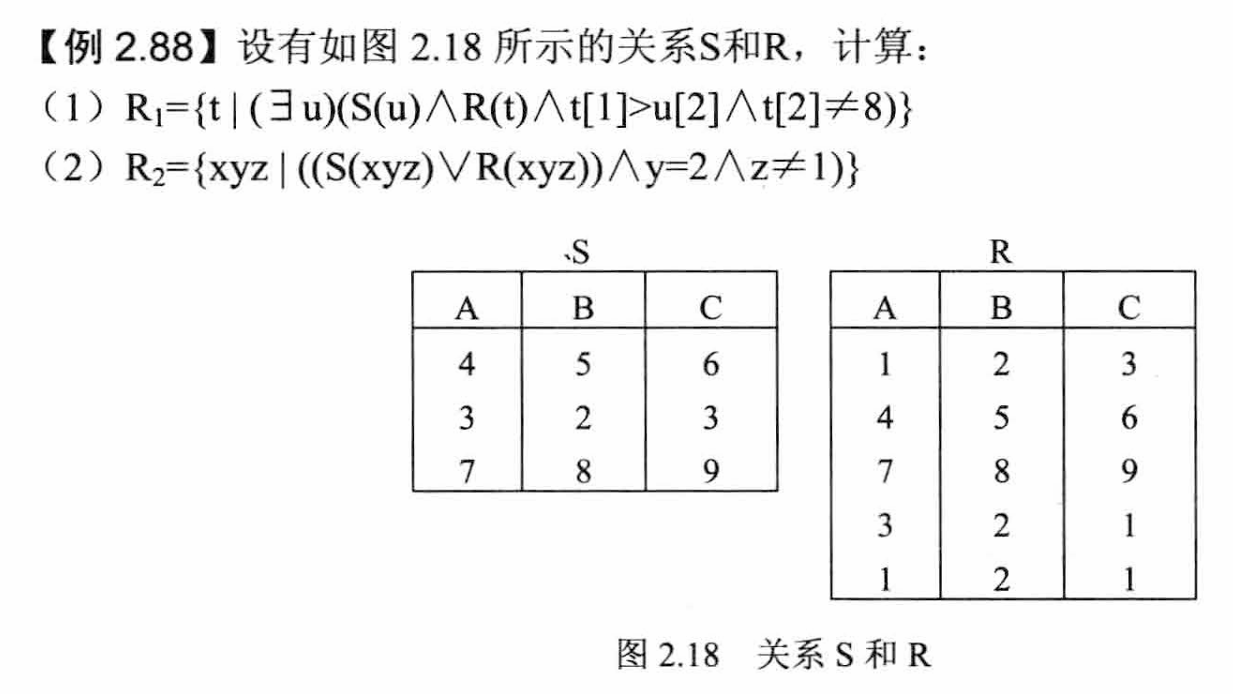
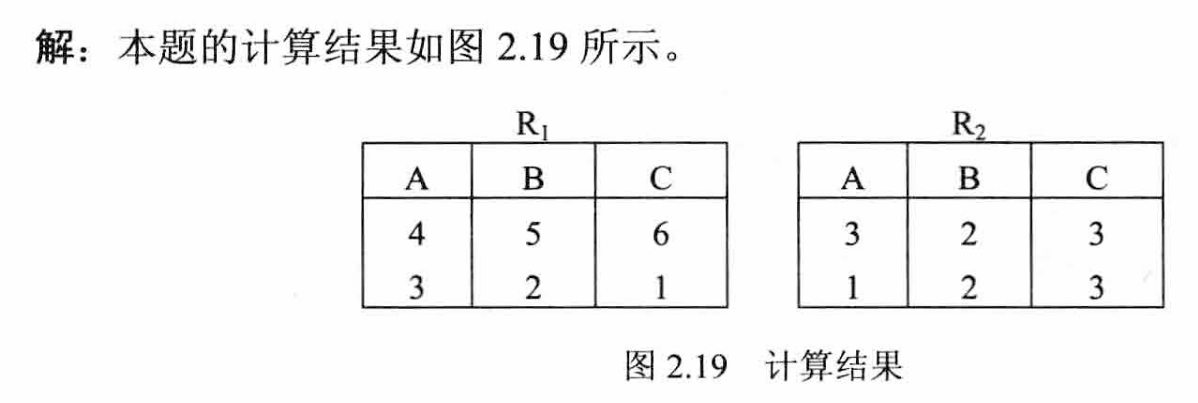
感觉不太好用言语形容为什么做出来的答案是这样（尤其是域关系演算），多做题吧。

同时，关系代数表达式也有自己的优先级：