数据库八股文——规范化理论
规范化理论
规范化理论的目的
不恰当的关系设计
有这样一个关系:in_dep (ID, name, salary, dept_name, building, budget),其中 ID 为主码。
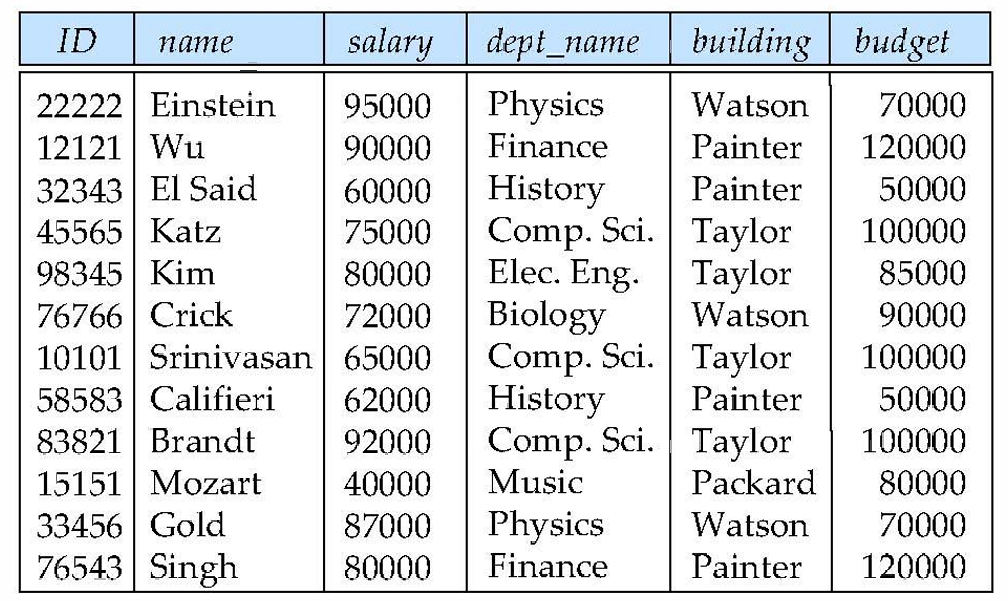
现在有以下四个问题:
- 重复性:属性 building 和 budget 出现了大量重复的值
- 更新:如果我仅仅更新了一个 building 的 budget,理论上所有对应的 budget 都应该被修改
- 插入:如果我仅仅插入一个新的 building 信息,则对于 instructor 部分只能取 NULL
- 删除:如果我删除了 instructor 的信息,building 相关信息也会消失
为什么会出现这些问题?
因为关系中出现了毫无关系的属性,也即 instructor 和 building 没有关联,却出现在了同一张表格中。
如何解决这些问题?
使用规范化理论约束关系的设计。
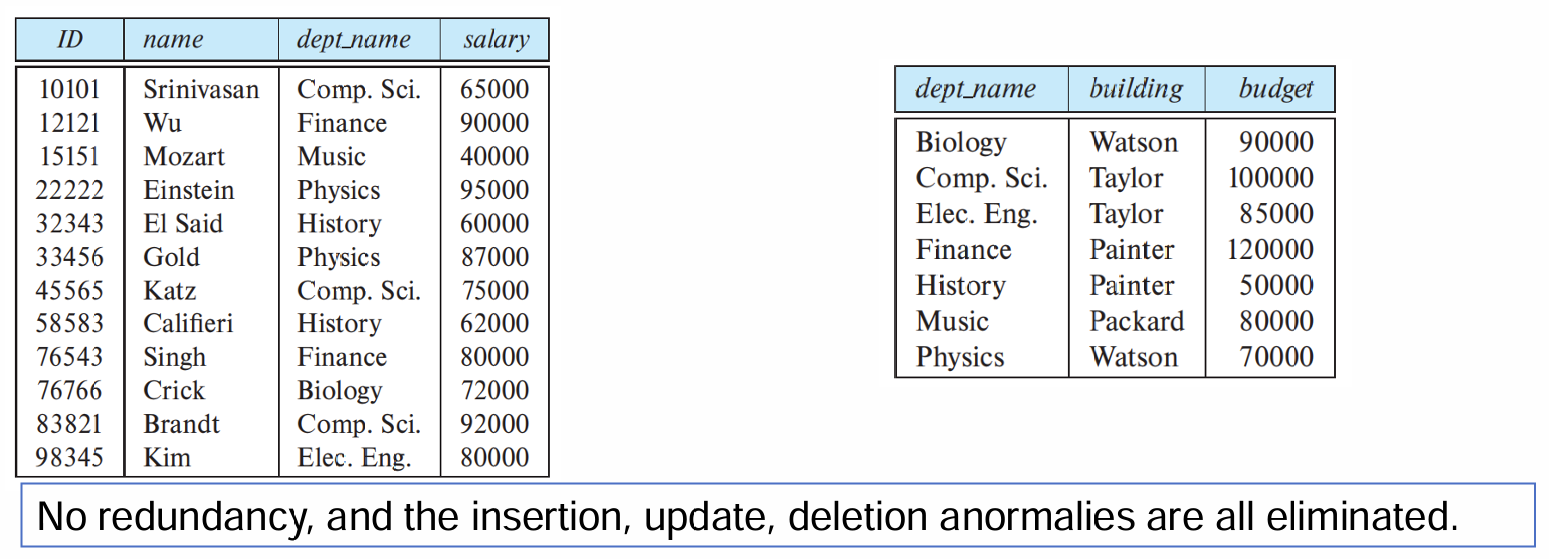
有损分解
上述例子通过拆分关系达到了约束效果,但实际上拆分不是随意的,例如下面这个例子:
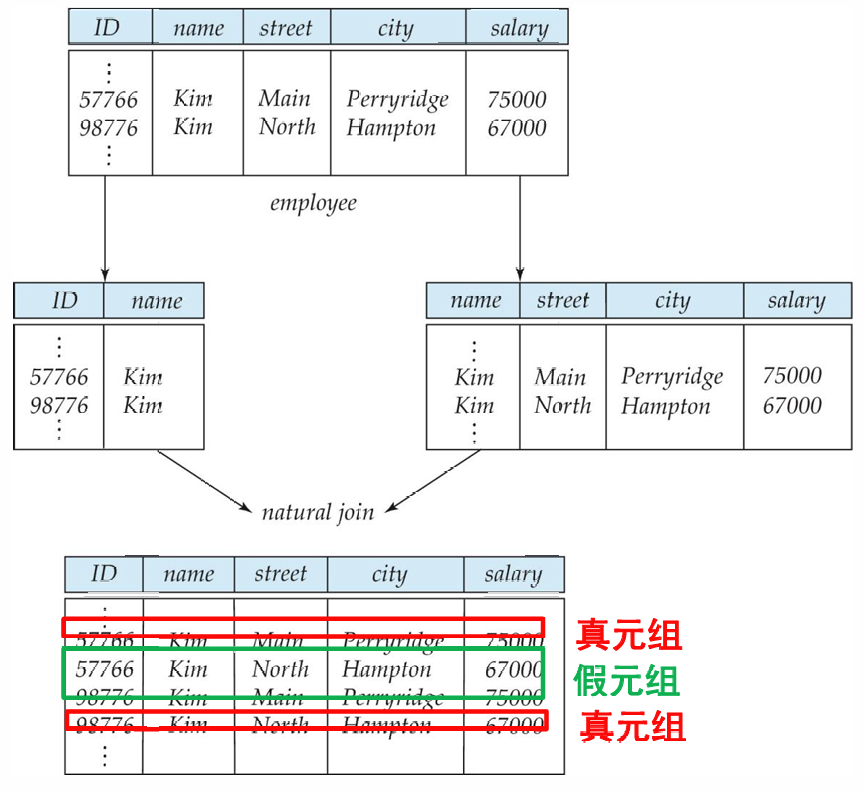
我们发现,拆分之后的表格重新组合后会多出一些不该存在的元组。我们称:如果一个分解不能组合成原来的样子(多元组/少元组),则该分解称为有损分解。
规范化的分解要求:
- 无损连接,分解后的关系可以拼接会原来的关系
- 依赖保持,通过规定分解后关系的约束,支持在分解前关系上存在的约束
规范化规则
函数依赖 Functional Dependencies
函数依赖反映了一个关系中属性或者属性组之间相互依存、相互制约的关系,即两个列或者列组之间的约束。
函数依赖起到检测冗余是否存在的作用,通过冗余的检测,就能很容易判断出这个关系是不是存在相应的插入,删除,更新异常。基于函数依赖理论,可以将一个关系分解为几个更小的关系,使之满足规范化程度更高的关系表。
设关系 R(U) 是一个在 U 属性集上定义的关系,X, Y 为 U 的两个子集:
若对于 R(U) 的任意一个可能的关系 r,r 中不可能存在两个元组在 X 上的属性值相等, 而在 Y 上的属性值不等。
则称:X → Y,X 称为这个函数依赖的决定属性集(Determinant)
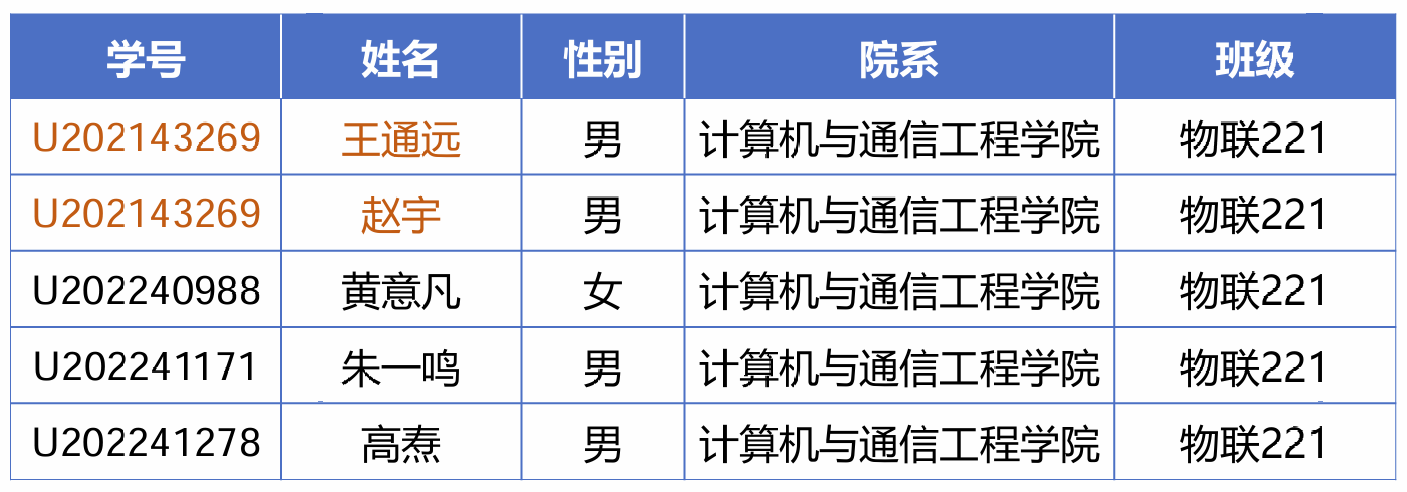
对于上图的关系,要求是属性 学号 → 姓名,也即只要知道了学号,就能推得姓名。上图中的黄色部分违反了这一规则人,因为相同的学号推得了不同的姓名,说明不能称 学号 → 姓名。
函数依赖和属性的关系
对于属性集 X 和 Y,他们的基数约束规则决定了他们之间可能的函数依赖。
- 一对一,则存在函数依赖 X → Y 和 Y → X
- 一对多,则存在函数依赖 Y → X
- 多对多,则不存在依赖
平凡函数依赖/非平凡函数依赖
如果 X → Y 并且 Y ⊆ X,则称 X → Y 是平凡的函数依赖,否则则称非平凡的函数依赖。
很明显,平凡的函数依赖是一句废话,所以我们一般研究的都是非平凡的函数依赖。
完全函数依赖/部分函数依赖
如果 X → Y,并且对于 X 的任何一个真子集 X’,都有X’ ⇏ Y,则称 Y 完全函数依赖于 X,记作 X →f Y,否则称 Y 部分依赖于 X,记作 X →P Y。
传递函数依赖
如果 X → Y,Y → Z,且 Y 不包含于 X,Y ⇏ X,则称Z传递函数依赖于 X,记作 X →T Z
如果 Y → X, 即 X ←→ Y (X Y 相互依赖),则 Z 直接依赖于 X
连接依赖
关系 R 的每个合法实例 r,都具有一个无损联结分解。也即任何的关系实例,都存在一组属性集上覆盖,使得其求投影后自然连接完全等价于原关系实例。
规范化设计与范式
在关系模式中存在函数依赖时就有可能存在数据冗余,进而可能导致数据操作异常。因此,关系表的规范化设计就是要尽可能地减少关系表中列或者列组之间的依赖关系,进而得到简洁独立的关系表。
关系表的规范程度状态为范式(nommalomm,NF),范式可以用于确保数据库模式中没有各种类型的异常和不一致,不同的规范化范式要求可以设计出几余程度不同的数据库。
规范化,就是指一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式集合。
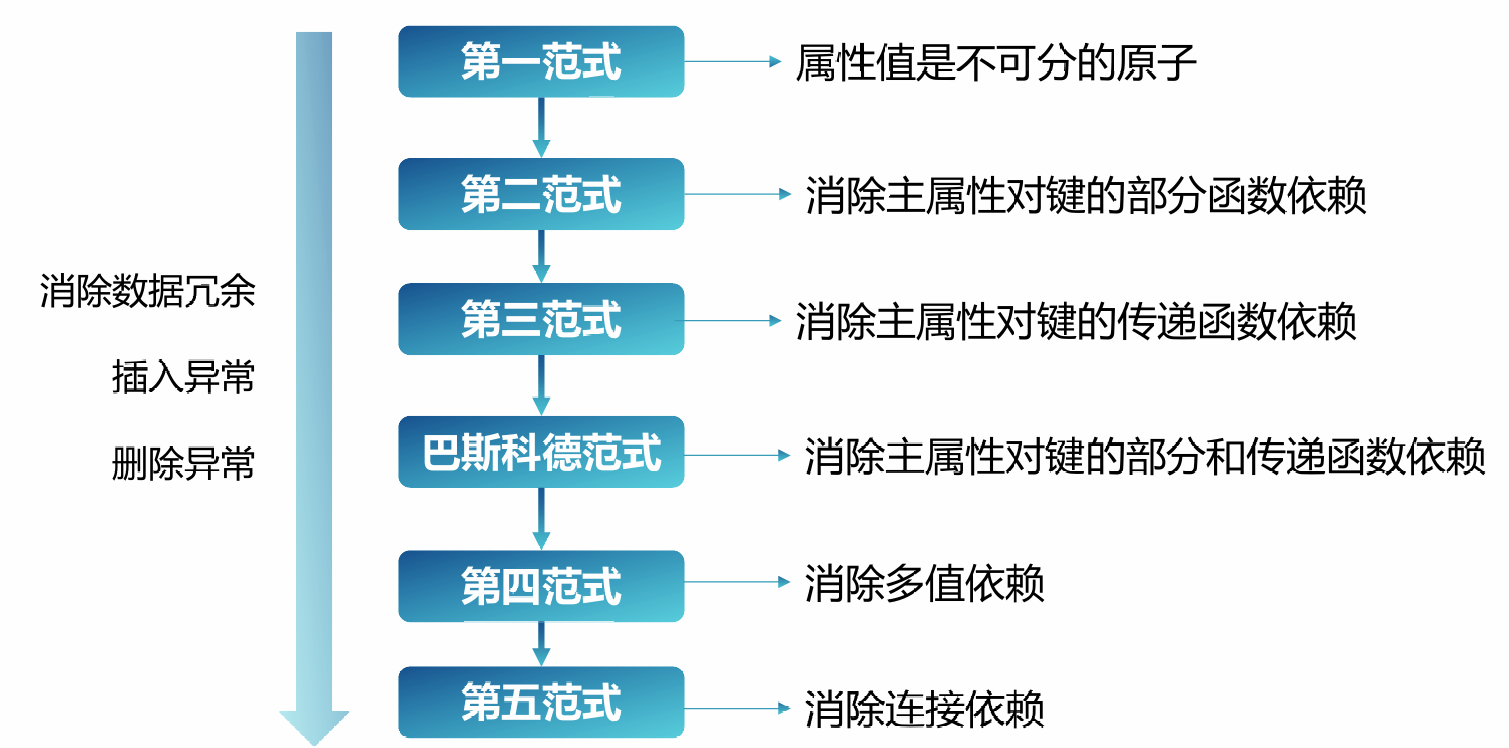
第一范式 —— 属性是不可再分的原子
第一范式(1NF)是指关系 R 的每一属性都是不可再分的基本数据项,同一属性中不能有多个值,即关系表中的某个属性不能有多个值或者不能有重复的属性。
在关系数据库中,满足最低要求的范式是第一范式,不满足第一范式的不是关系数据库。如果出现重复的属性,则根据第一范式,需要将该属性进行细分。
将不属于第一范式的关系规范化的方法:
- 在含有重复数据的那些行的空白列上输入合适的数据,也就是在需要填充的位置复制非重复的数据(对表的平板化处理)
- 将重复数据单独移动到一个新的关系中,同时也将原来关系中的关键属性(组)复制到这个新的关系中。如果有多个重复组或者重复组里又有重复组,反复使用这种方法,直到不再有重复组为止
第二范式 —— 非主属性完全函数依赖于候选码
每一行数据仅可以被候选码唯一区分
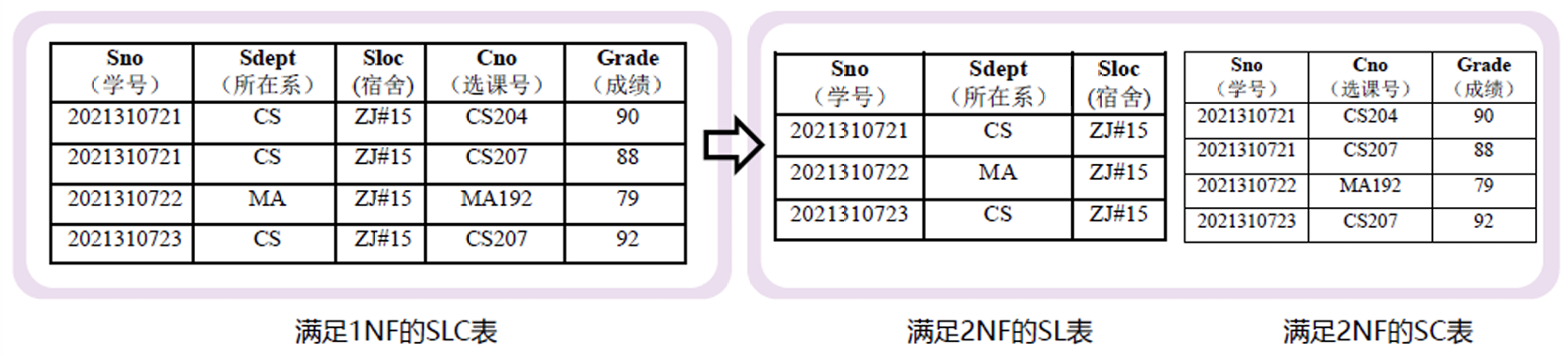
左侧关系中,候选码为 (Sno, Cno),有 (Sno, Cno) → Sdept, Sno → Sdept
不难发现 Sdept 部分依赖于候选码,该关系不属于第二范式
第三范式 —— 不存在传递依赖
在 2NF 基础上,消除依赖传递,任何非主属性不依赖与其他非主属性。即每个属性都和候选码有直接关系,不存在非主属性间的相互依赖。
在一个表中,如果一个非主属性依赖于另一个非主属性,那么当更新其中一个属性时,另一个属性可能会出现错误。
这可能会导致查询结果出现错误,也可能会使得对数据库的修改出现问题。我们需要保证只有更新候选码的时候才需要大规模的改动其他非主属性。
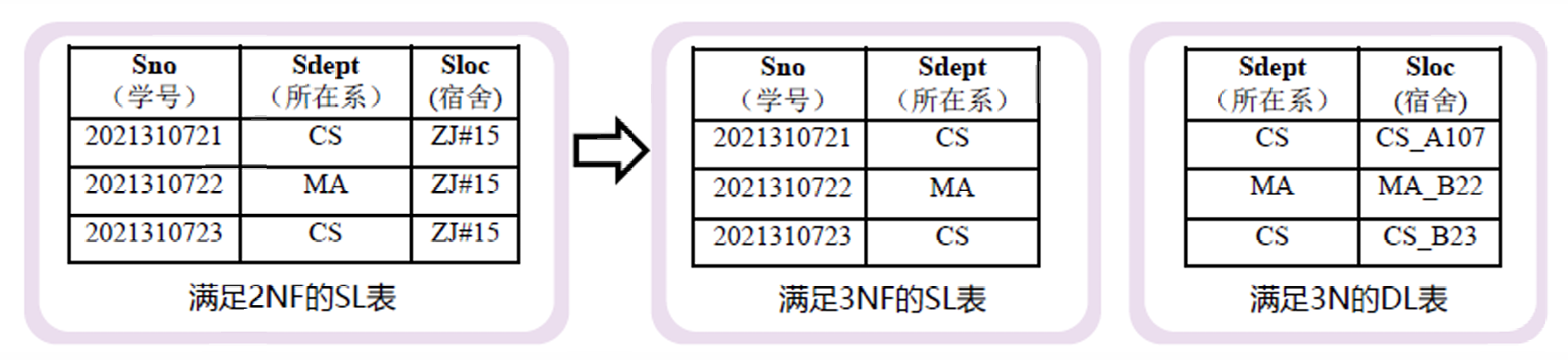
例如上图左侧的关系,存在函数依赖 Sno → Sdept, Sdept → Sloc, 故存在传递依赖 Sdept → Sloc,该关系不属于 3NF,但是并没有部分依赖于候选码的情况,故属于 2NF。
巴斯-科德范式 BCNF —— 依赖关系式左侧必定包含候选码
对于一个关系的函数依赖集合,BCNF 要求所有左侧的属性集都包含任意一个候选码。
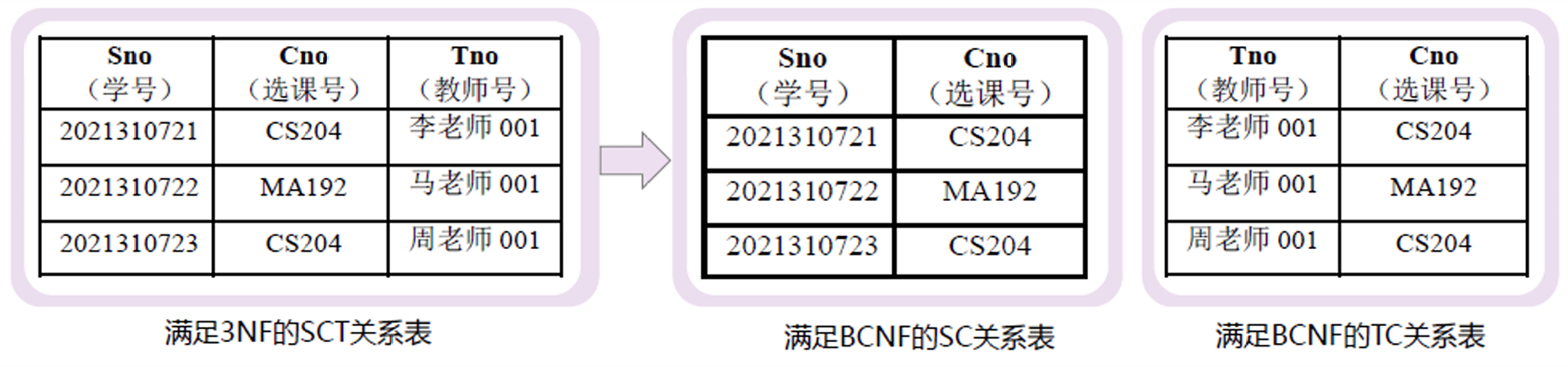
例如上图左侧的关系,假设每位教师只教一门课程,每门课程可以有若干教师讲授,那么每位学生选修某门课程就对应一位教师。存在函数依赖 Tno → Cno, (Sno, Cno) → Tno, (Sno, Tno) → Cno,候选码是 (Sno, Cno), (Sno, Tno),不存在非平凡的函数依赖,满足 3NF,但是 Tno 不包含任何一个候选码,不属于 BCNF。
- 满足 BCNF,一定满足 3NF
- 满足 3NF 并且只有一个候选码,一定满足 BCNF
- 所有非主属性都完全函数依赖于每个候选键
- 所有主属性都完全函数依赖于每个不包含它的候选键
- 没有任何属性完全函数依赖于非候选键的任何一组属性
数据依赖的公理系统 Armstrong System
逻辑蕴含定理
- 如果 Y 包含于 X,则 X → Y
- 如果 X → Y,则 XZ → YZ
- 如果 X → Y 并且 Y → X,则 X → Z
- 如果 X → Y 并且 X → Z,则 X → Z
- 如果 X → Y 并且 Z 属于 Y,则 X → Z
- 如果 X → Y 并且 YW → Z,则 XW → Z
例如依赖集合 {𝑈1 → 𝑈2𝑈3, 𝑈3𝑈4 → 𝑈5𝑈6},判断 𝑈1𝑈4 → 𝑈6是否正确
① 𝑈1 → 𝑈2𝑈3 => 𝑈1 → 𝑈3
② 𝑈1 → 𝑈3, 𝑈3𝑈4 → 𝑈5𝑈6 => 𝑈1𝑈4 → 𝑈5𝑈6
③ 𝑈1𝑈4 → 𝑈5𝑈6 => 𝑈1𝑈4 → 𝑈6
属性依赖闭包
U = {A1, A2, ⋯, An} 是关系模式 R 中所有属性的集合,F 是 U 上的一组函数依赖(即 R 的函数依赖集),X ⊆ U,Y ⊆ U,
XF+ = {Ai | X → Ai},称为该属性的依赖闭包。
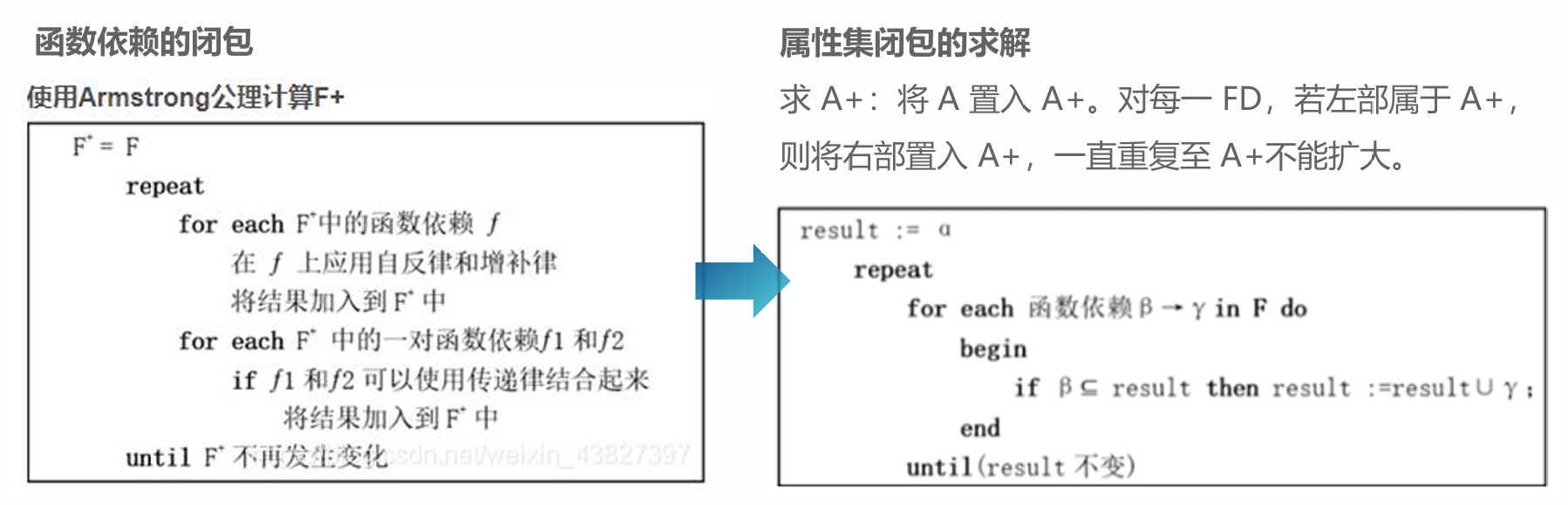

① 加入 A1, A5
② 找到左侧是 A1, A5 的子集的函数依赖
③ 加入 A3, A4
④ 找到左侧是 A1, A3, A4, A5 的子集的函数依赖
⑤ 加入 A6
⑥ 找到左侧是 A1, A3, A4, A5, A6 的子集的函数依赖
⑦ 没有变化,退出循环。结果为 {A1, A3, A4, A5, A6}
函数依赖闭包
在检验范式时,仅考虑给定的函数依赖集是不充分的,还需要考虑在给定的模式上成立的所有函数依赖关系。函数依赖集合 F,称 F+ 为 F 所能推得的全部函数依赖的集合,一般 F+ 中会有大量的重复函数依赖规则。
F = {A → B, B → C}, 求 F+
① 构造二维表
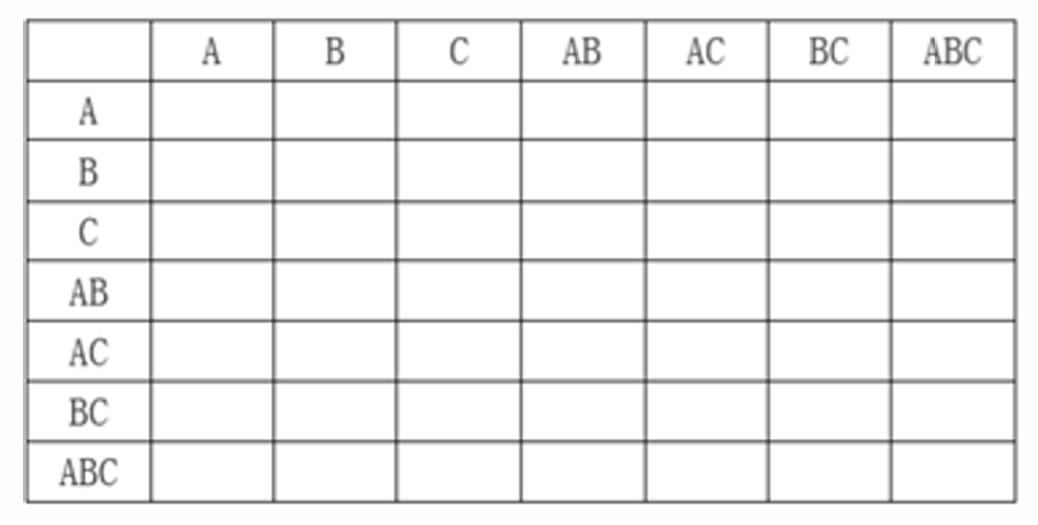
② 计算所有属性组合的属性集闭包,将表格中包括在对应属性闭包里的属性都勾选出来
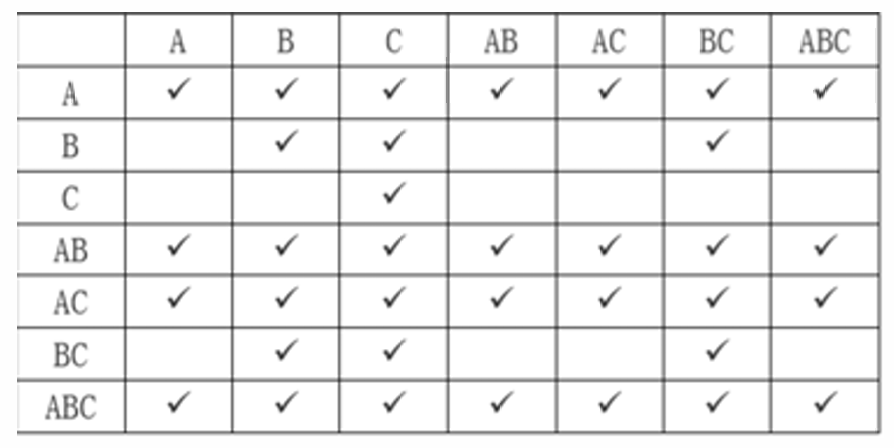
表格中任何一个 √ 都是一个函数依赖。
求解关系的候选键
- L 类属性:只在 F 中某个函数依赖的左部出现。
- R 类属性:只在 F 中某个函数依赖的右部出现。
- LR 类属性:在 F 中某个函数依赖的左部和右部均出现。
- N 类属性:在 F 中每个函数依赖左部和右部均不出现。
求解候选键的核心思路:
- 求解 L 和 N 类属性
- 若 (L, N)+ = U,则 (L, N) 为唯一候选键
- 若 (L, N)+ ≠ U,则找 LR 类
- 若 (L, N, LR)+ = U,则 (L, N, LR) 为候选键

① L = {A1}, N = {}, LR = {A2, A3, A4}
② 令 X = L, Y = LR
③ 计算 X 的闭包: XF+ = {A1} ≠ U
④ 遍历 Y 中的单一属性,并与 X 构成属性组,后计算闭包
- XA2F = (A1A2)F → A1A2A3A4A5A6,因此 {A1, A2} 是候选键
- XA3F = (A1A3)F → A1A2A3A4A5A6,因此 {A1, A3} 是候选键
- XA4F = (A1A4)F → A1A2A3A4A5A6,因此 {A1, A4} 是候选键
关系模式分解
最小函数依赖集
- 函数依赖的右侧只有单个属性
- 没有多余的函数依赖
- 函数依赖左侧没有多余的属性
计算最小函数依赖集
- 右部属性拆开:A → BC => A → B, A → C
- 左侧属性拆开:如果其他规则可以推得左侧属性集中的属性,删掉
- 如果有冗余规则,删掉
关系模式分解的定义
- 关系不丢失
- 模式不冗余
- 依赖不丢失
数据等价:分解具有无损连接性(lossless join),无损连接是指分解后的关系通过自然连接可以恢复分解前的关系,即通过自然连接得到的关系与分解前的关系相比,既不多出信息、又不丢失信息。
语义等价:分解要保持函数依赖(preserve functional dependency)。因此关系模式等价分解既要保持函数依赖,又要具有无损连接性。
无损的模式分解要求分解后关系自然连接的结果完全等同于原关系
无损分解
- 构建二维表格,纵向为关系,横向为属性
- 一行一行看,分解后关系所在行,将包含的属性置为 1,其余为 0
- 遍历全部函数依赖,对于依赖 A → B,如果 A 所属列全部为 1,则将 B 所属列全部置为 1
- 如果最后有任意一行全部为 1,说明是无损分解


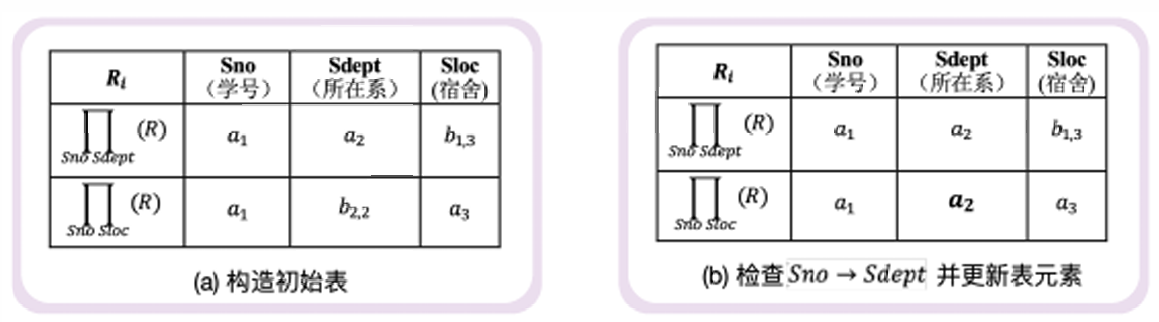
函数依赖保持

- 若一个分解具有无损连接性,则它能够保证不丢失信息
- 若一个分解保持了函数依赖,则它可以减轻或者解决各种异常情况
- 然而,无损分解和保持函数依赖的分解是两个相互独立的标准
- 具有无损连接性的分解不一定能够保持函数依赖
- 保持函数依赖的分解也不一定是无损分解